CEL analysis of a rotating water disk

This problem contains basic test cases for one or more Abaqus elements and features.

This page discusses:

ProductsAbaqus/Explicit

Elements tested

EC3D8R

Features tested

Eulerian analysis

Problem description

This example utilizes the pure Eulerian analysis technique to model viscous flow of water between two concentric cylinders.

Model:

The model is created using a simple circular Eulerian domain with an outer radius of 0.07 m and an inner radius of a = 0.04 m (see Figure 1). Because Eulerian analyses must be conducted in three-dimensional space, this two-dimensional problem is approximated using a thin domain with a single Eulerian element through its thickness. Rectangular-shaped elements provide the best accuracy and performance in Eulerian analyses, so the thickness is chosen to correspond to the minimum element size.

Mesh:

The Eulerian domain is meshed with 160 elements in the circumference and 14 elements along the radial direction (see Figure 1). The mesh provides good resolution in the radial direction and reasonable aspect ratio elements. A total of 2240 Eulerian EC3D8R elements are used. The circular (conforming) meshing is employed to avoid the need for Eulerian-Lagrangian contact.

Material:

Water is modeled as a nearly incompressible, viscous Newtonian fluid. The linear Us − Up Hugoniot form of the Mie-Grüneisen equation of state is used in the material model. The parameters used to define the material are listed in Table 1.

Boundary conditions:

To approximate the rotation of the water disk, the water is subjected to a uniform tangential velocity of U = 0.2932 m/s at the outer circumference and fixed at the inner circumference, as illustrated in Figure 1. Zero-velocity boundary conditions normal to all the domain faces prevent the flow of material into or out of the domain.

Results and discussion

The applied boundary conditions fully confine the water inside the Eulerian domain. Because the Us − Up material is nearly incompressible, care must be taken to ensure that the applied boundary conditions do not result in a volume change, which could induce spurious pressure oscillations in the water. Indeed, the prescribed tangential velocity is volume-preserving (tangential to the domain boundary) only in infinitesimal deformation. Finite displacement of the boundary nodes occurs in a straight line trajectory, not in a circumferential arc, which induces radial expansion as well as circumferential motion. The underlying Lagrange-plus-remap formulation of the EC3D8R element utilizes an intermediate “deformed” state, which includes this finite displacement (see Eulerian Analysis Techniques). This formulation results in large pressure oscillations that overshadow the viscous shear stresses of interest. The pressure is relieved by releasing the radial velocity at the inner radius, allowing infinitesimal radial motion to offset the radial components of prescribed velocity.

The analytical solution for the steady-state tangential velocity along the radius is given by Granger (1995) as

Vθ⁢(r)=U⁢ba2-b2⁢(a2r-r).

In Abaqus/Explicit the simulation begins with the water at rest, and the tangential velocity U is prescribed on the outer boundary. The velocity propagates radially inward via the viscosity and eventually reaches nearly steady-state conditions. With U = 0.2932 m/s, the water disk rotates one revolution in about 0.15 seconds. A simulation time of 3 seconds is chosen so that the water disk rotates 20 revolutions and the solution approximates the steady state. Figure 2 shows the solutions of the transient tangent velocities along the radius. After 20 revolutions the transient solution closely matches the analytic steady solution.

Without the pressure relief boundary modification, large pressures develop. Figure 3 shows the evolution of the pressure along the radius. The pressure experiences large oscillations at the beginning of the revolution of t = 0.015 seconds and rapidly increases with time. Indeed, the oscillation is also observed in the velocity curve close to the inner surface at t = 0.015 and 0.15 seconds. A positive tangent velocity here indicates that the water even flows in the reverse direction to the applied velocity close to the inner surface.

Figure 4 and Figure 5 show the evolution of the tangential velocity and pressure distributions along the radius with the boundary condition at the inner radius relieved so that the boundary nodes can move radially. The tangential velocity gradually approaches the analytical solution. The pressure is reduced by over three orders of magnitudes and oscillates about the analytical solution of a constant pressure of zero. The relieved boundary condition also speeds up the calculations by a factor of nearly 2.5 times. The relieved boundary at the inner radius results in a radial displacement of 4.32 × 10−6 m, or 0.01% of the inner radius the model, which can safely be ignored.

Considering the transient dynamic nature of Abaqus/Explicit, the tangential velocity profile after three seconds shows good accuracy compared to the steady-state analytical solution.

References

  1. Granger,  R.A., Fluid Mechanics, Dover Publications, 1995.

Tables

Table 1. Material parameters for water.
Parameter Value
Density (ρ) 998.2 kg/m3
Viscosity (η) 0.1 N⋅ s/m2
c0 1450 m/s
s 0 
Γ0 0 

Figures

Figure 1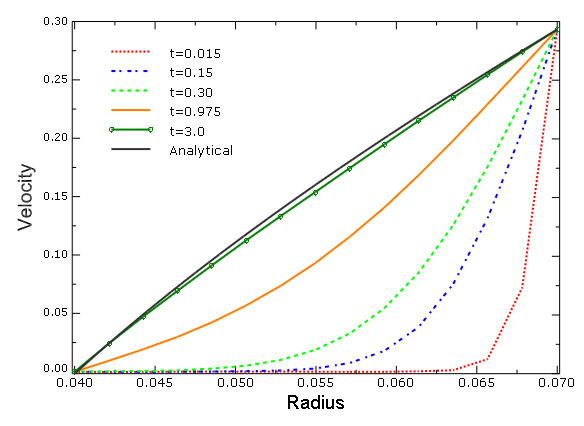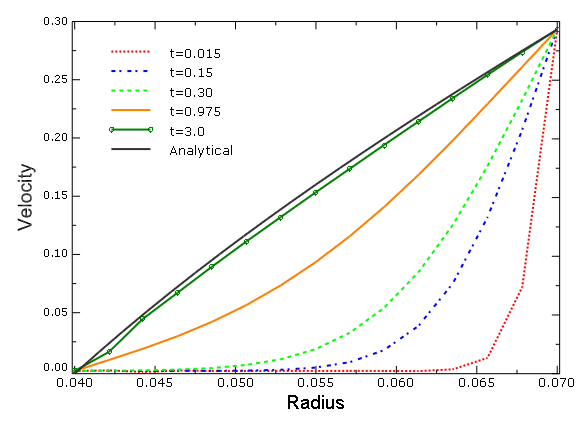. Geometry, mesh, and boundary conditions of the Eulerian domain.

Figure 2. Evolution of the tangential velocities without pressure relief.

Figure 3. Evolution of the pressure without pressure relief.

Figure 4. Evolution of the tangential velocities with relieved boundary condition at the inner radius.

Figure 5. Evolution of the pressure with relieved boundary condition at the inner radius.