Elements tested
C3D8R
CPS4R
CPE4R
ProductsAbaqus/Explicit Elements testedC3D8R CPS4R CPE4R Features testedBrittle cracking model response under simultaneous tension and shear loading: this verifies the shear retention formulation used in the model. Problem descriptionThis test illustrates the behavior of the brittle cracking model when subjected to simultaneous tension and shear loading. This behavior has been the subject of much discussion in the context of comparing different kinds of cracking models (fixed cracks versus rotating cracks, orthogonal cracks versus non-orthogonal cracks); see, for example, Rots and Blaauwendraad (1989). It has been argued that fixed orthogonal crack models, such as the one implemented in Abaqus/Explicit, produce shear behavior that is too stiff. In this verification example we show that this is not the case because of the manner in which the shear retention behavior is formulated in Abaqus/Explicit (as described in A cracking model for concrete and other brittle materials). The test carried out here was originally suggested by Willam et al. (1987). It consists of loading a specimen in the horizontal direction (direction 1) until a vertical crack initiates (Figure 1(a)); then the specimen is loaded simultaneously in biaxial tension and shear, as shown in Figure 1(b).The latter part of the loading causes the principal stress directions to rotate, and the issue is whether the cracking model provides an adequate shear response (the shear stress must vanish as deformation takes place). This test is carried out on six single elements that are all run in one input file. The original length of each side of the elements is . Figure 2 shows the six elements used in the analysis in their original and deformed shapes. The dashed lines illustrate the original shapes. The bottom row contains C3D8R, CPS4R, and CPE4R elements with shear retention properties defined using a power law analytical form, while the top row contains the same elements but with shear retention properties defined using a tabular form that mimics the analytical form. The purpose of testing the two groups of elements is to verify the two different options available in Abaqus/Explicit for defining shear retention. The material properties used are those of a typical medium strength concrete: the elastic properties are 30 × 109 Pa, 0.2; the cracking failure stress is 3 × 106 Pa; the shear retention is defined by the power law provided in Abaqus/Explicit with 2 and .001; and the mass density is 2400 kg/m3. Results and discussionFigure 3 shows horizontal stress-strain for the three different element types using the power law shear retention input definition. The results are identical for the three element types. Figure 4 shows horizontal stress-strain for the three different element types using the tabular shear retention input definition. The results are again identical for the three element types. In addition, comparing the results for the two different shear retention input definitions, we observe that they are identical. Figure 5 and Figure 6 show similar results for vertical stress-strain behavior. This horizontal and vertical stress-strain behavior obtained with the cracking model is a reflection of the input tension softening data, since the specimen cracks both in the horizontal and vertical directions. Figure 7 shows shear stress-strain for the three different element types using the power law shear retention input definition. The results are identical for the three element types. Figure 8 shows shear stress-strain for the three different element types using the tabular shear retention input definition. The results are again identical for the three element types. In addition, comparing the results for the two different shear retention input definitions, we observe that they are identical. We also observe that the model provides shear stress that increases to a maximum value (which depends on the shear retention properties) and then decreases to zero. This damage-like shear behavior is an important characteristic, and it has been claimed that rotating crack models provide it, while fixed crack models cannot. This test shows that the cracking model implemented in Abaqus/Explicit does produce this desired shear behavior. Input files
References
Figures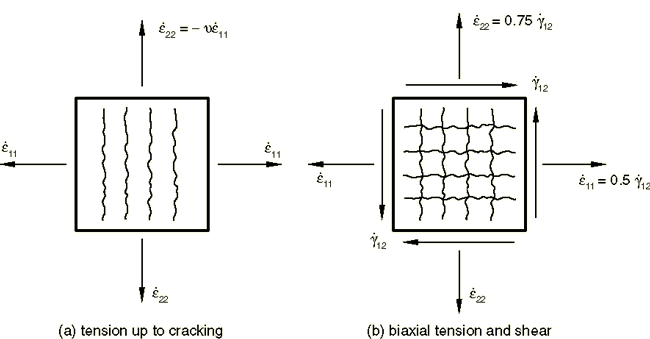 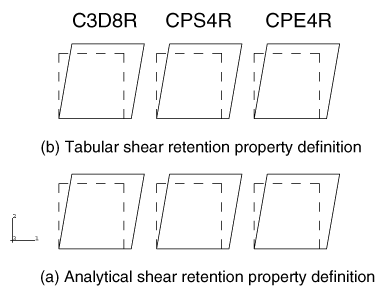 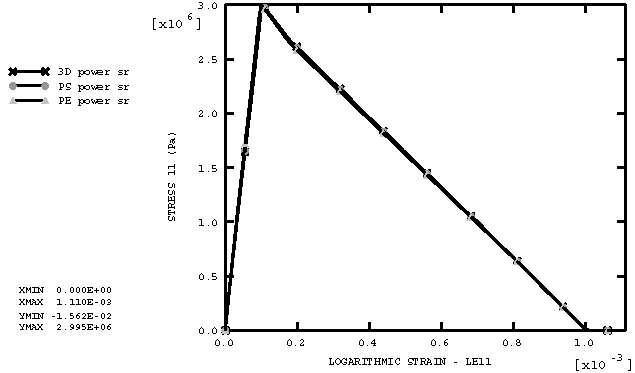  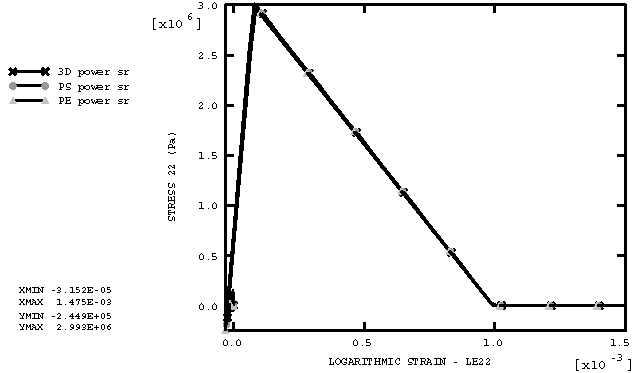 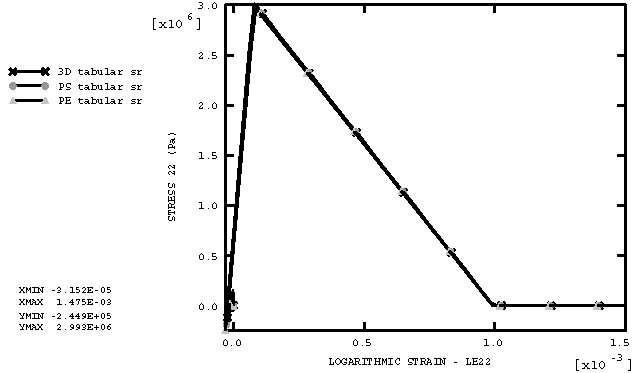   | |||||||