Mass proportional damping in Abaqus/Explicit

This problem contains basic test cases for one or more Abaqus elements and features.

This page discusses:

Elements tested
Features tested
Problem description
Results and discussion
Input files
Figures

ProductsAbaqus/Explicit

Elements tested

T3D2

Features tested

Mass proportional damping.

Problem description

This example is intended to verify mass proportional damping by comparing the Abaqus/Explicit results with an exact solution for a simple problem.

Mass proportional damping is defined by including damping in the material definition for those elements in which mass proportional damping is desired.

The example is the simplest dynamic system: a massless truss connecting a point mass to ground. The mass is obtained by giving the material in the truss a density so that the lumped mass of the truss gives the correct point mass at the free end of the truss. The truss is stretched initially and then relaxed so that it undergoes vibrations of small amplitude. The solution is compared with the exact solution obtained by solving the equation of motion analytically.

Figure 1 shows the geometry. The model consists of a single truss element, type T3D2, constrained at one node and free to move only in the x-direction at its other node. The truss's mass matrix is lumped; therefore, the system is equivalent to a spring and a lumped mass. The cross-sectional area of the truss is 645 mm² (1 in²), and its length is 254 mm (10 in). It is made of linear elastic material, with a Young's modulus of 69 GPa (10⁷ lb/in²). The density of the truss provides a lumped mass at the unrestrained end of 2.777 × 10⁵ kg (1585 lb-s²/in).

The mass is displaced by 25.4 mm (1 in) in the first step by stretching the free end and then released in the second step. The time histories are plotted and compared with the theoretical value.

Results and discussion

The equation of motion for the system is

m \ddot{u} + c \dot{u} + k u = 0,

where m is the mass, $c (= α m)$ is the damping, $α$ is the mass damping factor, k is the stiffness, and u is the displacement.

Assuming a solution of the form $u (t) = u_{0} \exp λ t$ , we have

λ = \frac{- c}{2 m} \pm \sqrt{{(\frac{c}{2 m})}^{2} - ω_{u}^{2}},

where $ω_{u} = \sqrt{k / m}$ is the undamped frequency of vibration. Critical damping occurs when the value of c causes the discriminant of this equation to be zero so that

c_{c} = 2 m ω_{u} = 2 \sqrt{k m} .

We define the damping ratio, $ξ$ , as the ratio of damping to critical damping:

ξ = \frac{c}{c_{c}} = \frac{α}{2 ω_{u}} .

The relationships in this equation are often used as a basis for choosing $α$ and $β$ .

The equation defining $λ$ can be rewritten

λ = ω_{u} (- ξ \pm \sqrt{ξ^{2} - 1}) .

We choose the damping in this case to be less than critical, $ξ = $ 0.02 $<$ 1, and the system can vibrate. The initial conditions are $u (0) = $ 1 and $\dot{u} (0) = $ 0; therefore, the dynamic part of the motion is

u (t) = \exp (- ξ ω_{u} t) (\frac{ξ}{\sqrt{1 - ξ^{2}}} \sin ω_{d} t + \cos ω_{d} t),

where $ω_{d} = ω_{u} \sqrt{1 - ξ^{2}}$ is the damped frequency of the system.

To generate damping with $ξ = $ 0.2, a mass proportional damping factor of $α = $ 1.00472 sec⁻¹ is used. A variable mass proportional damping can also be defined by specifying the damping coefficient as a tabular function of temperature and/or field variables in Abaqus/Explicit. The parameters used in the theoretical results can be calculated as $ω_{u} = $ 25.11802 rad/sec, $ω_{d} = $ 25.11300 rad/sec, and

u (t) = \exp (- 0.5023603 t) (0.020004001 \sin 25.113 t + \cos 25.113 t) .

The displacement value at the end of Step 2 (t=2.5 sec) is 0.2841910 in; Abaqus/Explicit gives 0.2717 in with a 4% relative error. For this one-element simple truss model, direct user control of the incrementation through the dynamic step is used to achieve smooth and accurate results. The displacement history is compared with the analytical result in Figure 2.

Input files

massdamping.inp: Input data used in this analysis.

Figures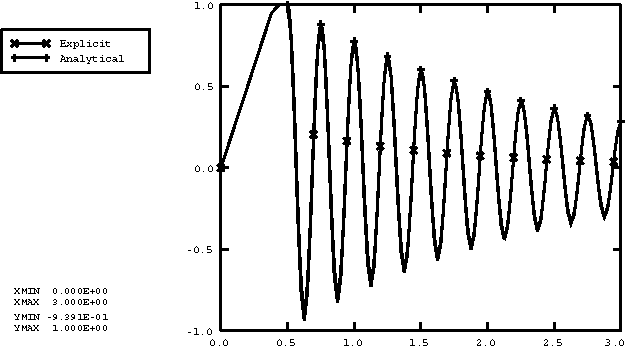