Elements tested
- CPE3T
- CPE4H
- CPE4RT
- CPE6MH
- CPE8H
- CPE8HT
- C3D4H
- C3D8H
- C3D10H
- C3D10HS
- C3D10MH
- C3D20H
ProductsAbaqus/StandardAbaqus/Explicit Elements tested
Features testedContact pair Surface on a deformable body that may contact itself Problem descriptionThe tests exercise the self-contact capability that is available for finite-sliding surfaces by declaring a single surface name in conjunction with a contact pair. The models consist of a deformable ring with an inside radius of 2.0 and an outside radius of 3.0. The ring rests on a flat rigid surface. A circular indenter, represented by another analytical rigid surface, is initially in contact with the ring at a point. This indenter has a radius of 1.0 and is diametrically opposed to the flat surface. Contact pairs define contact between the outside surface of the ring and the two rigid surfaces and between the inside surface of the ring and itself. The ring is modeled with plane strain elements: 4-node quadrilaterals, 6-node modified triangles, or 8-node quadrilaterals. In the Abaqus/Standard simulations the elements use a hybrid formulation to accommodate an incompressible neo-Hookean hyperelastic material. Although the inside surface of the ring is closed, open surfaces are tested by eliminating one element of the inside perimeter from the surface definition, as shown in Figure 1. The loading consists of two steps. In the first step the indenter moves down enough to produce self-contact of the inside surface (Figure 2). In the second step the indenter is simultaneously translated (−10.0 in the horizontal direction) and rotated (−8.0 around its center) in such a way that it makes the ring roll along the flat rigid surface (Figure 3). This produces a continuously changing region of contact. Traction is provided by setting the coefficient of friction to 0.5 for the rigid surface interfaces. One case tests coupled thermal-mechanical interfaces. The ring is divided in two halves. The top half is given an initial temperature of 100.0, and the bottom half is given an initial temperature of 0.0. Heat transfer is allowed at the interface involving the inside surface. The two steps map into a time of 100.0 units each. This is the only case that is also solved with Abaqus/Explicit. In the Abaqus/Explicit simulations both CPE3T and CPE4RT elements are used to model the ring; four elements are used through the thickness of the ring, and 72 elements are used around its circumference. A small amount of compressibility is added to the material definition, and mass scaling is used to obtain an efficient solution. Nondefault hourglass control is also used to control element hourglassing. Material:
Results and discussionSelf-contact is established and evolves over large portions of the single surface. This class of problems would be difficult to analyze with portions of the inside surface defining a conventional contact pair. The temperature results for the coupled thermal-mechanical interface tests obtained with Abaqus/Explicit agree with those obtained with Abaqus/Standard. The stresses predicted by the two analysis products differ slightly in this case since a fully incompressible material is modeled in Abaqus/Standard while a slightly compressible one is modeled in Abaqus/Explicit. Input filesAbaqus/Standard input files
Abaqus/Explicit input files
Figures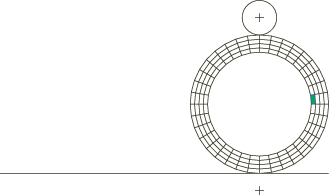  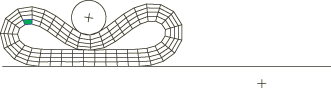 | |||||||||||||||||||||||||||||||||||||