Elements tested
CPE4R
SPRINGA
MASS
DASHPOTA
ProductsAbaqus/Explicit Elements testedCPE4R SPRINGA MASS DASHPOTA Features testedTime integration procedure, nonlinear springs and dashpot, distributed loads, point loads, gravity loading. Problem descriptionThere are six individual single degree of freedom spring-mass systems defined in this problem. In each case two springs are attached to a single CPE4R element that is constrained to have only vertical motion. The meshes are shown in Figure 1. The following cases are considered:
Results and discussionFigure 2 shows the displacement of each single degree of freedom system as a function of time. Cases 1, 2, and 3 have identical solutions and match the analytical solution for the single degree of freedom system. Case 6 shows smaller amplitudes of oscillation due to the damping effect of the dashpot. Case 4 matches the analytical solution for the added mass. Case 5 has no analytical solution; however, the results are qualitatively correct. Input files
Both input files are designed to provide identical results. Figures 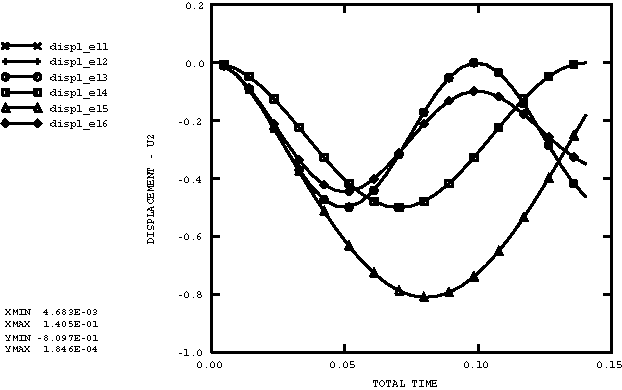 | |||||||