Temperature-dependent elastic materials

This problem contains basic test cases for one or more Abaqus elements and features.

This page discusses:

Elements tested
Features tested
Problem description
Results and discussion
Input files
Tables
Figures

ProductsAbaqus/Explicit

Elements tested

T2D2

T3D2

B21

B31

PIPE21

PIPE31

SAX1

S4R

S4RS

S4RSW

C3D8R

C3D10M

CPE4R

CPE6M

CPS4R

CPS6M

CAX4R

CAX6M

M3D4R

Features tested

Temperature-dependent material properties with predefined temperature fields are tested for the following elastic material models: isotropic elasticity, orthotropic elasticity, anisotropic elasticity, and lamina.

Problem description

This verification test consists of a set of single element models that include combinations of all the available element types with all the available material models. All the elements are loaded with a tensile load defined by specifying the vertical velocity at the top nodes of each element with the bottom nodes fixed. The velocity is ramped from zero to 0.2. The temperature at all nodes increases from an initial value of 0° to a final value of 100°. The material properties are defined as a linear function of temperature, as shown in Table 1. The density for all the materials is 7850. For every material model, only those element types available for the model are used. The undeformed meshes are shown in Figure 1.

Results and discussion

Figure 2 shows the plot of vertical stress versus vertical strain for the isotropic elasticity model. The plots of vertical stress versus vertical strain for orthotropic elasticity (ENGINEERING CONSTANTS), orthotropic elasticity (ORTHOTROPIC), anisotropic elasticity, and lamina are shown in Figure 3, Figure 4, Figure 5, and Figure 6, respectively. The vertical stress and vertical strain are $σ_{11}$ and $ϵ_{11}$ for the truss, beam, and axisymmetric shell elements and $σ_{22}$ and $ϵ_{22}$ for the remaining elements. The results from pipe elements are consistent with the beams.

Input files

temp_elastic.inp: Input data used in this analysis.
temp_elastic_ef1.inp: External file referenced in this analysis.
temp_elastic_simpson.inp: Explicit dynamics analysis using Simpson integration through the shell thickness.
temp_elastic_restart.inp: Restart data that completes 25 milliseconds of the response.

Tables

Table 1. Material properties.
Material	Properties	T=0	T=100
Isotropic elasticity	E	193.1 × 10⁹	97.0 × 10⁹
	$ν$	0.0	0.0
Orthotropic elasticity	$E_{1}$	2.0 × 10¹¹	1.0 × 10¹¹
(ENGINEERING CONSTANTS)	$E_{2}$	1.0 × 10¹¹	5.0 × 10¹⁰
	$E_{3}$	1.0 × 10¹¹	5.0 × 10¹⁰
	$ν_{12}$	0.0	0.0
	$ν_{13}$	0.0	0.0
	$ν_{23}$	0.0	0.0
	$G_{12}$	7.69 × 10¹⁰	6.69 × 10¹⁰
	$G_{13}$	7.69 × 10¹⁰	6.69 × 10¹⁰
	$G_{23}$	9.0 × 10⁹	8.0 × 10⁹
Orthotropic elasticity	$D_{1111}$	2.24 × 10¹¹	1.00 × 10¹¹
(ORTHOTROPIC)	$D_{1122}$	4.79 × 10⁵	4.59 × 10⁵
	$D_{2222}$	1.23 × 10¹¹	0.5 × 10¹¹
	$D_{1133}$	4.21 × 10⁵	4.00 × 10⁵
	$D_{2233}$	4.74 × 10⁵	4.00 × 10⁵
	$D_{3333}$	1.21 × 10¹¹	0.5 × 10¹¹
	$D_{1212}$	7.69 × 10¹⁰	7.00 × 10¹⁰
	$D_{1313}$	7.69 × 10¹⁰	7.00 × 10¹⁰
	$D_{2323}$	9.00 × 10⁹	8.00 × 10⁹
Lamina	$E_{1}$	2.0 × 10¹¹	1.0 × 10¹¹
	$E_{2}$	1.5 × 10¹¹	0.7 × 10¹¹
	$ν_{12}$	0.0	0.0
	$G_{12}$	2.00 × 10¹⁰	1.80 × 10¹⁰
	$G_{13}$	9.00 × 10⁹	8.00 × 10⁹
	$G_{23}$	8.50 × 10⁹	7.50 × 10⁹
Anisotropic elasticity	$D_{1111}$	2.24 × 10¹¹	1.00 × 10¹¹
	$D_{1122}$	4.79 × 10⁵	4.00 × 10⁵
	$D_{2222}$	1.23 × 10¹¹	0.5 × 10¹¹
	$D_{1133}$	4.21 × 10⁵	4.00 × 10⁵
	$D_{2233}$	4.74 × 10⁵	4.00 × 10⁵
	$D_{3333}$	1.21 × 10¹¹	0.5 × 10¹¹
	$D_{1112}$	1.00 × 10⁶	9.00 × 10⁵
	$D_{2212}$	2.00 × 10⁶	1.80 × 10⁶
	$D_{3312}$	3.00 × 10⁶	2.60 × 10⁶
	$D_{1212}$	7.69 × 10¹⁰	7.00 × 10¹⁰
	$D_{1113}$	4.00 × 10⁶	3.60 × 10⁶
	$D_{2213}$	5.00 × 10⁶	4.60 × 10⁶
	$D_{3313}$	6.00 × 10⁶	5.60 × 10⁶
	$D_{1213}$	7.00 × 10⁶	6.60 × 10⁶
	$D_{1313}$	7.69 × 10¹⁰	7.00 × 10¹⁰
	$D_{1123}$	8.00 × 10⁶	7.60 × 10⁶
	$D_{2223}$	9.00 × 10⁶	8.00 × 10⁶
	$D_{3323}$	1.00 × 10⁷	9.00 × 10⁶
	$D_{1223}$	1.10 × 10⁷	1.00 × 10⁷
	$D_{1323}$	1.20 × 10⁷	1.10 × 10⁷
	$D_{2323}$	9.00 × 10⁹	8.00 × 10⁹

Figures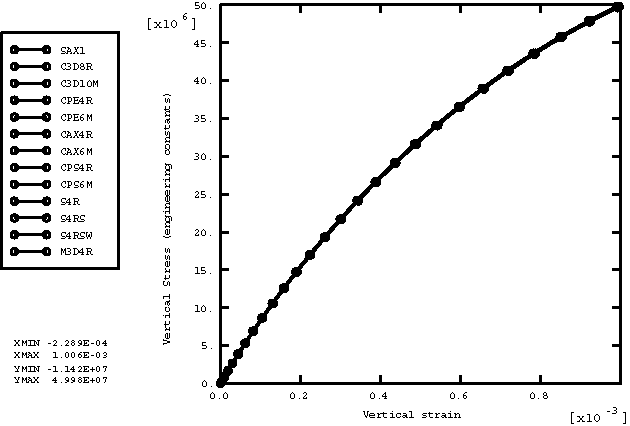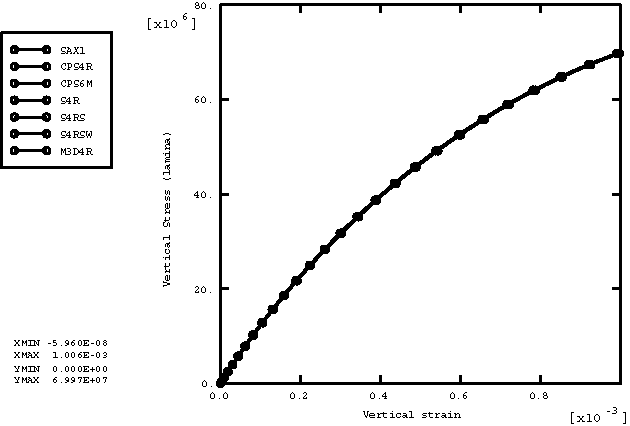