Elements tested
T2D2
T3D2
B21
B31
PIPE21
PIPE31
SAX1
S4R
S4RS
S4RSW
C3D8R
CPE4R
CPS4R
CAX4R
M3D4R
ProductsAbaqus/Explicit Elements testedT2D2 T3D2 B21 B31 PIPE21 PIPE31 SAX1 S4R S4RS S4RSW C3D8R CPE4R CPS4R CAX4R M3D4R Features testedTemperature-dependent material properties with predefined field variables are tested for the following inelastic material models: Mises plasticity, Drucker plasticity, Hill's potential plasticity, crushable foam plasticity with volumetric hardening, crushable foam plasticity with isotropic hardening, ductile failure plasticity, rate-dependent Hill's potential plasticity, rate-dependent Mises plasticity, Drucker-Prager/Cap plasticity, and porous metal plasticity. Problem descriptionThis verification test consists of a set of single-element models that include combinations of all of the available element types with all of the available material models. All of the elements are loaded with a tensile load defined by specifying the vertical velocity at the top nodes of each element with the bottom nodes fixed. The temperature at all nodes of each element increases from an initial value of 0° to a final value of 100°. The material properties are defined as a linear function of temperature. For every material model only those element types available for the model are used. The undeformed meshes are shown in Figure 1, and the material properties are listed in Table 1. Results and discussionFigure 2 shows the history plot of Mises stress for the Mises plasticity model for all elements, except for pipe elements, which are consistent with beams. We can see the material softening because the yield stress drops as the temperature increases. Figure 3 through Figure 11 show the history plots of Mises stress for the other material models. This problem tests the features listed but does not provide independent verification of them. Input files
Tables
Figures  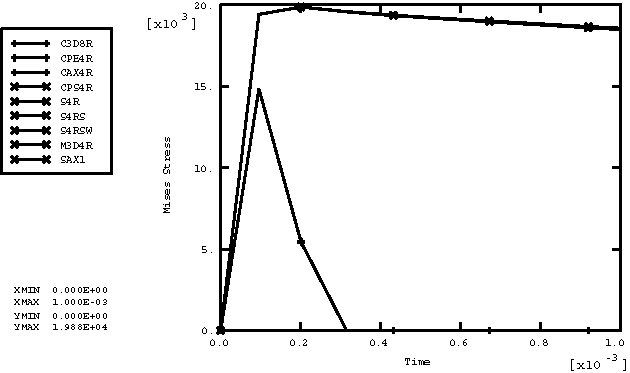 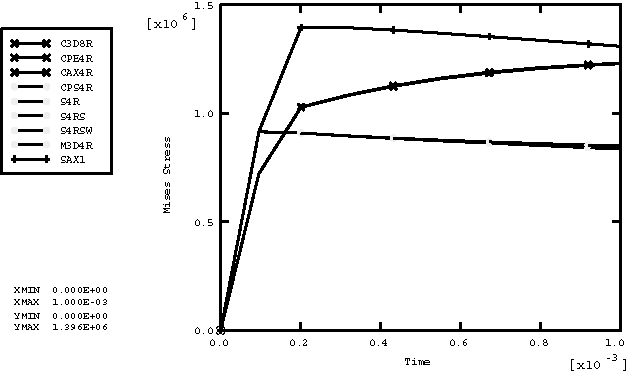 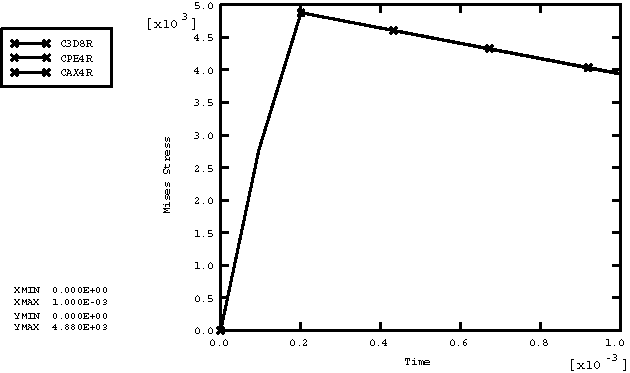  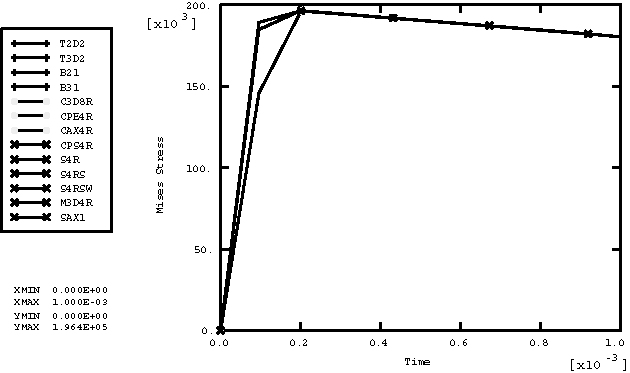   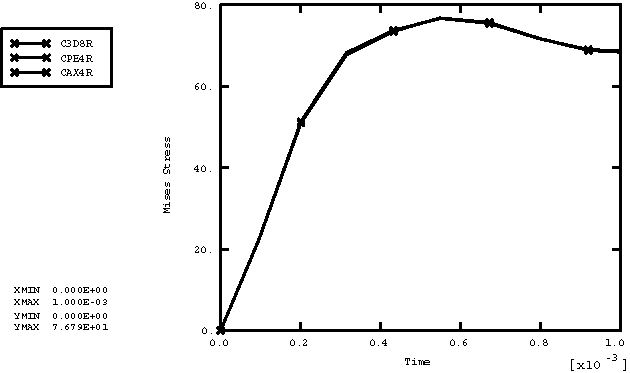  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||