Simple load tests for thermal-electrical elements

This problem contains basic test cases for one or more Abaqus elements and features.

This page discusses:

ProductsAbaqus/Standard

Elements tested

  • DC1D2E
  • DC1D3E
  • DC2D3E
  • DC2D4E
  • DC2D6E
  • DC2D8E
  • DCAX3E
  • DCAX4E
  • DCAX6E
  • DCAX8E
  • DC3D4E
  • DC3D6E
  • DC3D8E
  • DC3D10E
  • DC3D15E
  • DC3D20E

Problem description

The problem illustrated in Figure 1 consists of a 1-m-long conductor through which a constant current density of 6.58E5 Am−2 is established by creating a potential difference across the ends of the conductor or by prescribing a concentrated current. The electrical energy generated by the flow of current is converted into heat, which results in a temperature distribution through the conductor. Only a steady-state solution is considered for each test. A reasonable mesh is used in each case to obtain the quadratic distribution of heat.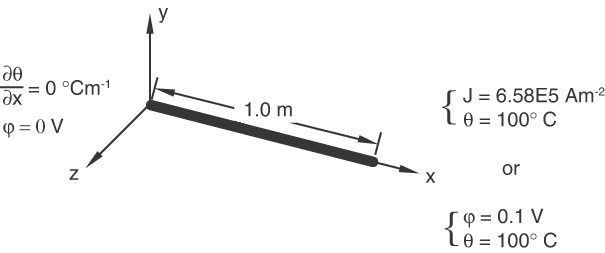

Figure 1. Model of conductor.

Material:

Thermal conductivity = 45 W/m°C; electrical conductivity = 6.58E6 1/Ω m.

Boundary conditions:

Zero potential (φ=​ 0 V) and zero temperature gradient (∂⁡θ/∂⁡x=​ 0°Cm−1) at x=​ 0 m.

Potential φ=​ 0.1 V and temperature θ=​ 100°C, or current density of 6.58E5 Am−2 and temperature θ=​ 100°C at x=​ 1 m.

With these boundary conditions the problem is one-dimensional. It is assumed that all electrical energy is converted into heat.

Reference solution

In this uniaxial problem the exact solution for the temperature is of the form θ=C0⁢x22+C1⁢x+C2, where C0, C1, and C2 are real constants. Application of the above material properties and boundary conditions leads to the exact solution

θ=C0⁢x22+100-C02,

where C0=​ −1462.2.

Results and discussion

The tests are composed of three steps.

In Step 1 the proper temperature boundary conditions are applied, and the flow of current is obtained by a potential difference between the two ends of the conductor. The coupled thermal-electrical procedure is used to obtain the desired temperature distribution across the conductor. For first-order elements the results are a function of y and z when the mesh generated is skewed in the x–y plane and/or the x–z plane. For the different test cases studied, the temperature may vary by as much as 3% in the y–z plane for a given x-value. Therefore, special care is needed when using triangular and tetrahedral elements. The exact solution is recovered in most test cases, with a maximum deviation of 1.5% from the exact solution observed with the DC3D6E elements. For second-order elements the exact results are obtained since the results are at most a quadratic function of the variable x. Moreover, skewed meshes do not affect the results.

Step 2 is a heat transfer step in which the conductor is allowed to cool down.

Step 3 invokes a coupled thermal-electrical procedure in which the same amount of electrical energy as that of Step 1 is provided to the specimen. However, energy is now supplied by specifying a prescribed current at x=​ 1 m instead of a potential of 0.1 V. Here again, the temperature results are identical to those obtained in Step 1, and the potential distribution that served as input for Step 1 is retrieved as output in this step.