Finite-strain consolidation of a two-dimensional solid

This example illustrates the large-scale consolidation of a two-dimensional solid. Nonlinearities caused by the large geometry changes are considered, as well as the effects of the change in the void ratio on the permeability of the material. The material is assumed to be linear elastic. The example exhibits many features in common with the one-dimensional Terzaghi consolidation problem discussed in The Terzaghi consolidation problem, notably the reduced settlement magnitudes predicted by finite-strain analysis in comparison with the results provided by small-strain theory.

This page discusses:

ProductsAbaqus/Standard

Problem description

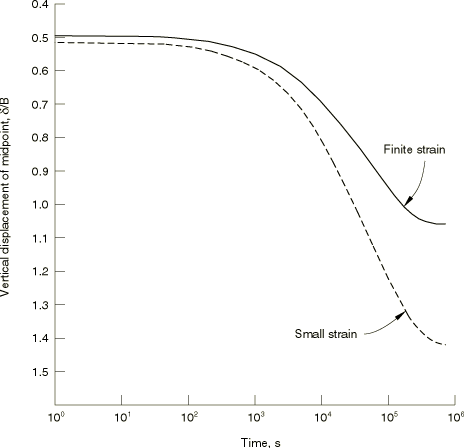
The example considers a finite strip of soil, loaded over its central portion. Symmetry permits modeling half the strip, as shown in Figure 1: the half-width of the strip is equal to its height, and the ratio of the loaded portion of the strip to the width of the strip is 1:5. The finite element discretization used is also shown in Figure 1: 35 CPE8RP elements are used, and the mesh is graded in the vertical direction in length ratios 1:2:3:4:5 and horizontally in ratios 1:1:1:2:2:4:4. This is a coarse mesh, but it is expected to provide representative results. A similar mesh using CPE4P elements is included for verification purposes.

Figure 1 also summarizes the material properties and boundary conditions used. The ratio of the pressure load to the Young's modulus is 1:2, and the Poisson's ratio is specified as 0. The soil is assumed to have an initial void ratio of 1.5, and the permeability at this value of the void ratio is 0.508 μm/sec (2.0 × 10−5 in/sec). The permeability is assumed to be one order of magnitude smaller at a void ratio of 1.0. These low permeability values are representative of clays.

The strip of soil is assumed to lie on a rigid, impermeable, smooth base. No horizontal displacement or pore fluid flow is permitted along the vertical sides of the model. Free drainage is assumed along the top surface of the model.

Loading and time stepping

The analysis is performed using two transient soils consolidation steps. In the preliminary step the full load is applied over two equal fixed time increments. The load remains constant in the subsequent step during which the soil undergoes consolidation.

In the analysis accounting for finite-strain effects, the preliminary step requires six iterations for convergence of the first increment and seven iterations for convergence at full load. These relatively large numbers of iterations are due to the large geometry changes experienced by the soil. As shown in Figure 2, at full load the midpoint vertical deflection in this case is about 0.49 times the width of the strip that is loaded. The geometrically linear analysis predicts the midpoint vertical deflection to be approximately 0.52 times the width of the strip that is loaded.

Practical consolidation analyses require solutions across several orders of magnitude of time (see Figure 2, for example), and the automatic time stepping scheme is designed to generate cost-effective solutions for such cases. The algorithm is based on the user supplying a tolerance on the pore pressure change permitted in any increment, Δ⁢uwm⁢a⁢x. Abaqus uses this value in the following manner: if the maximum change in pore pressure at any node is greater than Δ⁢uwm⁢a⁢x, the increment is repeated with a proportionally reduced time step. If the maximum change in pore pressure at any node is consistently less than Δ⁢uwm⁢a⁢x, the time step is increased. In this case Δ⁢uwm⁢a⁢x is set to 0.103 MPa (15 lb/in2). This represents about 3% of the maximum pore pressure in the model following application of the load. With this value the first time increment is 7.2 seconds, and the final time increment is 1853 seconds. This is quite typical of diffusion processes: at early times the time rates of pore pressure are significant, and at later times these time rates are very low.

Results and discussion

The first analysis considers finite-strain effects, and the soil permeability varies with the void ratio. This change of permeability with the void ratio is physically realistic—as soil is compressed, it becomes harder for pore fluid to flow through it. A small-strain analysis is also run with constant permeability. The midpoint settlement versus time for the finite- and small-strain analyses are shown in Figure 2. The two analyses predict large differences in the final consolidation: the small-strain result shows about 40% more deformation than the finite-strain case. This is consistent with results from the one-dimensional Terzaghi consolidation solutions—(see The Terzaghi consolidation problem). Quite clearly, in cases where settlement magnitudes are significant, finite-strain effects are important.

The time scale in Figure 2 spans five orders of magnitude, pointing to the importance of automatic time incrementation for cost-effective solutions.

Figure 3 shows time histories of pore pressure at two points in the model, points a and b in Figure 1. The pore pressure results are normalized by the value of pore pressure at these points at the end of the preliminary step and are taken from the finite-strain analysis. The increase in pore pressure shown at point b is evidence of the Mandel-Cryer effect (see Prevost, 1981 and Lambe and Whitman, 1969) and is typical of two- and three-dimensional consolidation analysis.

References

  1. Lambe,  T. W.,  and R. V. Whitman, Soil Mechanics, John Wiley and Sons, New York, 1969.
  2. Prevost,  J. H., “Consolidation of an Elastic Porous Media,” Journal of the Engineering Mechanics Division, ASCE, vol. 107, pp. 169–186, February 1981.

Figures

Figure 1. Two-dimensional elastic consolidation problem description.

Figure 2. Midpoint settlement time history.

Figure 3. Pore pressure time history.