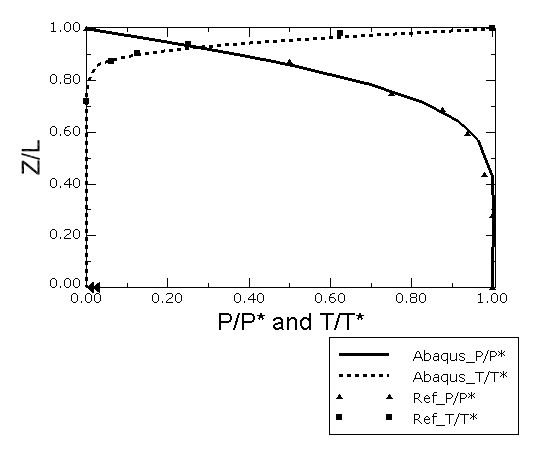
Problem description
This problem can be considered as the thermal counterpart to The Terzaghi consolidation problem. The discussion presented in that section is equally applicable to this problem and is not repeated here. Figure 1 shows one-dimensional thermoelastic consolidation of a linear elastic soil column under constant surface pressure and constant surface temperature. The column is 7 units high and 2 units wide. The bottom of the column is restrained, and all sides of the column are impermeable except for the top surface where free flow is allowed. The top surface is subjected to a constant pressure of 1 unit and a constant temperature of 50 units. The soil is assumed to be fully saturated. Gravity is neglected. The material properties reported by Aboustit et al. (1985) are used. The soil is elastic with a modulus of 6000 units and Poisson's ratio of 0.4. The permeability of the soil is 4 × 10−6 units with a specific weight of 1 unit. Since Aboustit et al. (1985) used only one set of thermal properties, identical thermal properties for the solid and the pore fluid are used. The specific heat is 40 units, and the density is 1 unit. The conductivity of the soil as well as the pore fluid is 0.2 units, and the coefficient of thermal expansion is 0.3 × 10−6.
All displacements perpendicular to the sides are restrained to enforce one-dimensional behavior. The consolidation analysis is performed using a transient soils consolidation step with automatic time stepping. The time stepping for this problem is controlled by two parameters: one that controls the accuracy of time integration for the temperature field, and one that controls the accuracy of time integration for the pore fluid flow. The stability limit for the pore fluid solution is given by
which dictates the minimum time increment. Variables used in this equation are defined in Coupled Pore Fluid Diffusion and Stress Analysis. The mesh used is identical to the one used by Aboustit et al. (1985), which led to a minimum time increment of 0.1. Because of the applied surface load, the elements near the surface immediately acquire a pore pressure equal to the applied load; hence, a maximum pore pressure change per increment of 1.1 with an initial time increment of 0.1 is used. This ensures that time steps smaller than 0.1 are not used in the analysis to satisfy time integration accuracy for pore fluid flow. The value for the maximum allowable temperature change in an increment was chosen as 3 to avoid having to use time increments that were smaller than what the stability limit for pore fluid required. The value for the maximum allowable temperature change was obtained by first running the problem using only the value for the maximum pore pressure change and determining the incremental temperature change. The parameter values listed above result in a moderately accurate solution. If a more accurate solution is desired, a more refined mesh should be used.
Nonlinear geometric effects are not important in this problem due to small load magnitudes. Similarly due to very small fluid velocities, heat convection effects due to pore fluid flow are not dominant enough to necessitate the inclusion of unsymmetric stiffness. However, for completeness, we have chosen to activate geometric nonlinear analysis as well as unsymmetric stiffness. Results of small-strain analysis with symmetric stiffness are indistinguishable from the results presented. The time period for the step is 21.1, corresponding to the time at which the Abaqus/Standard results are compared to the reference solution.