Debonding behavior of a single leg bending specimen

This example examines the debonding behavior of a single leg bending specimen.

The following Abaqus features are demonstrated:

predicting debond growth in a single leg bending (SLB) specimen using crack propagation analysis with the VCCT fracture criterion in Abaqus/Standard;
predicting debond growth using the VCCT fracture criterion and surface-based cohesive behavior in Abaqus/Explicit; and
predicting progressive delamination growth at the interface in this specimen subjected to sub-critical cyclic loading using the fatigue crack growth criterion based on the Paris law.

This page discusses:

Application description
Abaqus modeling approaches and simulation techniques
Case 1 Two-dimensional single leg bending model
Case 2 Three-dimensional single leg bending model
Case 3 Fatigue prediction using the same model as in Case 1
Case 4 Fatigue prediction using the same model as in Case 2
Case 5 Using VCCT in Abaqus/Explicit to model crack initiation
Input files
References
Figures

Application description

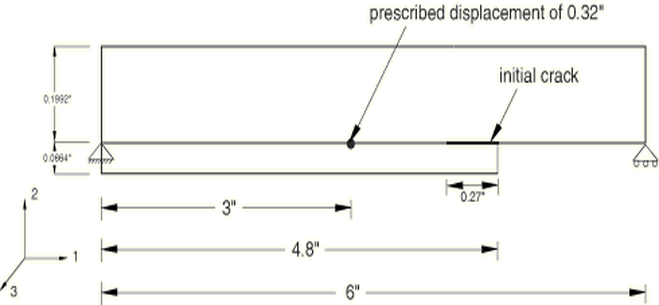
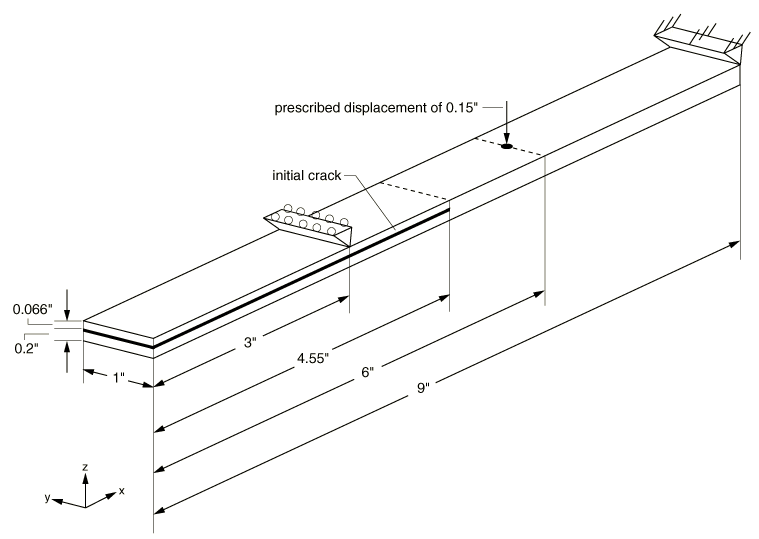
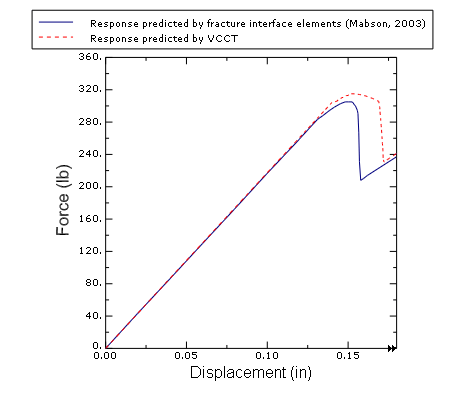
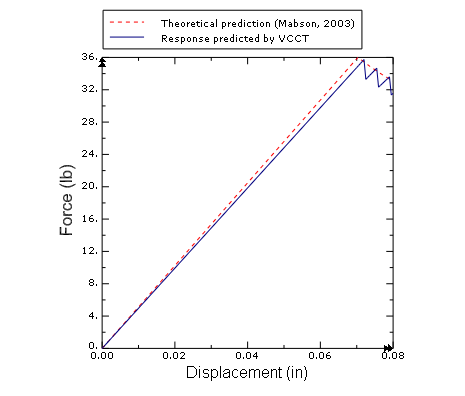
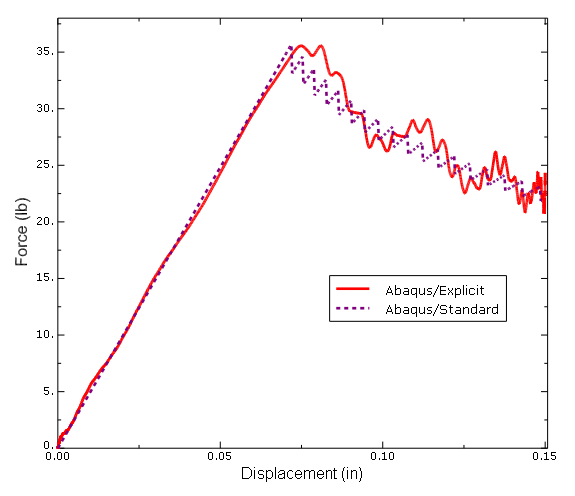
The example examines the debonding behavior of a single leg bending specimen and compares the simulation results with the results of the analysis performed using the VCCT-based fracture interface elements discussed in Mabson (2003). Damping is also used in a two-dimensional model to demonstrate how it can stabilize the crack growth.

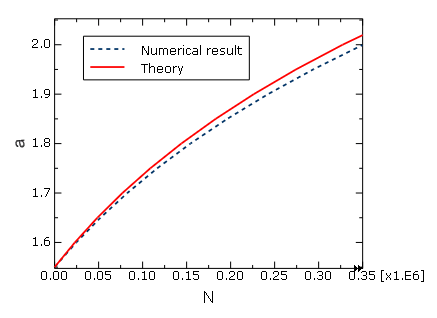
The same model is analyzed using the fatigue crack growth criterion to assess the fatigue life when the model is subjected to sub-critical cyclic loading. The onset and delamination growth are characterized using the Paris law, which relates the relative fracture energy release rate to the crack growth rate. The fracture energy release rate at the crack tip is calculated based on the VCCT technique. The results from Abaqus are compared with those predicted by the theory in Davidson (1995).

Geometry

The geometries of the two-dimensional and three-dimensional single leg bending specimens with their corresponding initial crack locations are shown in Figure 1 and Figure 2, respectively.

Boundary conditions and loading

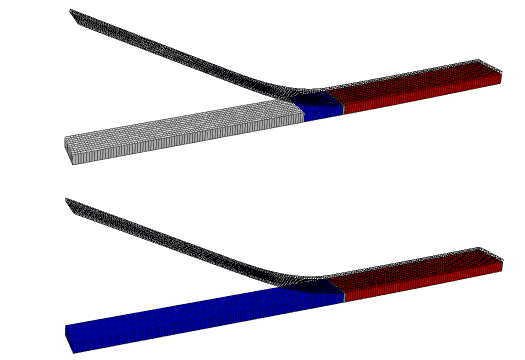
A displacement is applied on the top beam at the location shown in Figure 1 for the two-dimensional model and in Figure 2 for the three-dimensional model. The displacement results in a mixture of opening (mode I) and shearing (mode II) modes. The maximum displacements are set equal to 0.32 in (8.13 mm) in the two-dimensional model and 0.15 in (3.81 mm) in the three-dimensional model for the monotonic loading cases. In the fatigue crack growth analyses, cyclic displacement loadings with peak values of 0.12 in (3.05 mm) in the two-dimensional model and 0.035 in (0.89 mm) in the three-dimensional model are specified.

Abaqus modeling approaches and simulation techniques

This example includes one two-dimensional model and one three-dimensional model.

Summary of analysis cases


Case 1	Two-dimensional single leg bending model.
Case 2	Three-dimensional single leg bending model.
Case 3	Fatigue prediction with the direct cyclic approach and the linear elastic fatigue crack growth approach using the same model as in Case 1.
Case 4	Fatigue prediction with the direct cyclic approach and the linear elastic fatigue crack growth approach using the same model as in Case 2.
Case 5	Abaqus/Explicit with VCCT using the same model as in Case 2.

Analysis types

Static analyses are performed for Cases 1–4. Dynamic analysis is used for Case 5.

Case 1 Two-dimensional single leg bending model

This case compares the AbaqusVCCT results for the two-dimensional model with the results of Mabson (2003). The damping effects are also examined.

Mesh design

The model uses a finite element mesh of 4-node bilinear plane strain quadrilateral, incompatible mode elements (CPE4I) for both the long and short beams.

Results and discussion

Figure 3 shows the deformed configuration of the two-dimensional model. Figure 4 shows a contour plot of bond status variable BDSTAT that illustrates the debonding growth in a two-dimensional model. The region of debonding is shown on the right side of the model. Figure 5 compares the results from the two-dimensional analysis with the results of the analysis performed using the VCCT-based fracture interface elements discussed in Mabson (2003).

The damping effect to a two-dimensional simulation is also examined in this case by adding damping at the debond interface (see Automatic Stabilization of Rigid Body Motions in Contact Problems). The damping stabilizes the crack growth and allows the solution to converge. It is important to assess how much energy has been used for numerical damping by comparing the stabilization energy to the strain energy of the model. Figure 6 shows the comparison between static stabilization energy (ALLSD) and the strain energy of the model (ALLSE). The comparison indicates that the maximum static stabilization energy is less than 3% of the maximum strain energy of the model during the analysis. This value is reasonable and indicates that the solution has not been affected by the addition of artificial numerical damping.

Case 2 Three-dimensional single leg bending model

This case compares the AbaqusVCCT results for the three-dimensional model with a theoretical prediction.

Mesh design

The model uses fully integrated first-order shell elements (S4) for both the long and short beams.

Results and discussion

Figure 7 shows a contour plot of bond status variable BDSTAT for the three-dimensional model. Figure 8 shows a comparison between the results from the three-dimensional analysis and the results presented in Mabson (2003).

Case 3 Fatigue prediction using the same model as in Case 1

This case verifies that delamination growth in a two-dimensional single leg bending model subjected to sub-critical cyclic loading can be predicted using the fatigue crack growth criterion. Both the direct cyclic approach and the linear elastic fatigue crack growth approach are used in this case. The simulation results for the direct cyclic approach are compared with the theoretical results. Similar results are obtained with the linear elastic fatigue crack growth approach.

Mesh design

The mesh design is the same as in Case 1.

Results and discussion

The results in terms of crack length versus the cycle number obtained using the fatigue crack growth criterion in Abaqus are compared with the theoretical results in Figure 9. Reasonably good agreement is obtained.

Case 4 Fatigue prediction using the same model as in Case 2

This case verifies that delamination growth in a three-dimensional single leg bending model subjected to sub-critical cyclic loading can be predicted using the fatigue crack growth criterion with the debonding force removed immediately or ramped down gradually. Both the direct cyclic approach and the linear elastic fatigue crack growth approach are used in this study. The simulation results using the direct cyclic approach are compared with the theoretical results. Similar results are obtained when using the linear elastic fatigue crack growth approach.

Mesh design

The mesh design is the same as in Case 2.

Results and discussion

The results in terms of crack length versus the cycle number obtained using the fatigue crack growth criterion in Abaqus are compared with the theoretical results in Figure 10. Reasonably good agreement is obtained.

Case 5 Using VCCT in Abaqus/Explicit to model crack initiation

This case verifies that delamination growth can be predicted using Abaqus/Explicit. The simulation results are compared with results obtained from Abaqus/Standard. To reduce inertia effects and allow a better comparison between Abaqus/Standard and Abaqus/Explicit results, the material density was lowered and the loading was ramped on with a smooth step definition.

Mesh design

The mesh design is the same as in Case 2.

Results and discussion

The results obtained using Abaqus/Explicit with VCCT show reasonably good agreement with those obtained from Abaqus/Standard, as depicted in Figure 11 and Figure 12. Due to the thin layer of elements and the specified boundary conditions in the model, inertia effects are clearly observed in the measured reaction forces. However, the peak forces at debond onset, debond time, and other VCCT output quantities are consistent between the two analyses. The reaction forces obtained in Abaqus/Explicit were filtered with a Butterworth filter with a cutoff frequency of 500 Hz to reduce high-frequency oscillations from the response curve.

Input files

slb_vcct_2d_1.inp: Two-dimensional model of the SLB specimen.
slb_vcct_3d_1.inp: Three-dimensional model of the SLB specimen.
slb_vcct_fatigue_2d.inp: Same as slb_vcct_2d_1.inp but subjected to cyclic displacement loading using the direct cyclic approach.
slb_vcct_fatigue_2d_2_simp.inp: Same as slb_vcct_2d_1.inp but subjected to cyclic displacement loading using the simplified fatigue crack growth approach.
slb_vcct_fatigue_2d_3_simp_tabular.inp: Same as slb_vcct_2d_1.inp but subjected to cyclic displacement loading using the simplified fatigue crack growth approach with the tabular form.
slb_vcct_fatigue_2d_3_simp_user.inp: Same as slb_vcct_2d_1.inp but subjected to cyclic displacement loading using the simplified fatigue crack growth approach with the user-defined subroutine.
slb_vcct_fatigue_2d_3_tabular.inp: Same as slb_vcct_2d_1.inp but subjected to cyclic displacement loading using the general fatigue crack growth approach with the tabular form.
slb_vcct_fatigue_2d_3_user.inp: Same as slb_vcct_2d_1.inp but subjected to cyclic displacement loading using the general fatigue crack growth approach with the user-defined subroutine.
slb_vcct_fatigue_3d.inp: Same as slb_vcct_3d_1.inp but subjected to cyclic displacement loading using the direct cyclic approach.
slb_vcct_fatigue_3d_2_simp.inp: Same as slb_vcct_3d_1.inp but subjected to cyclic displacement loading using the simplified fatigue crack growth approach.
slb_vcct_fatigue_3d_3_simp_tabular.inp: Same as slb_vcct_3d_1.inp but subjected to cyclic displacement loading using the simplified fatigue crack growth approach with the tabular form.
slb_vcct_fatigue_3d_3_simp_user.inp: Same as slb_vcct_3d_1.inp but subjected to cyclic displacement loading using the simplified fatigue crack growth approach with the user-defined subroutine.
slb_vcct_fatigue_3d_3_tabular.inp: Same as slb_vcct_3d_1.inp but subjected to cyclic displacement loading using the general fatigue crack growth approach with the tabular form.
slb_vcct_fatigue_3d_3_user.inp: Same as slb_vcct_3d_1.inp but subjected to cyclic displacement loading using the general fatigue crack growth approach with the user-defined subroutine.
slb_vcct_fatigue_3d_3_simp_tabular_ramp.inp: Same as slb_vcct_fatigue_3d_3_simp_tabular.inp but with the debonding force ramped down gradually.
slb_vcct_fatigue_3d_3_simp_user_ramp.inp: Same as slb_vcct_fatigue_3d_3_simp_user.inp but with the debonding force ramped down gradually.
slb_vcct_fatigue_3d_3_tabular_ramp.inp: Same as slb_vcct_fatigue_3d_3_tabular.inp but with the debonding force ramped down gradually.
slb_vcct_fatigue_3d_3_user_ramp.inp: Same as slb_vcct_fatigue_3d_3_user.inp but with the debonding force ramped down gradually.
slb_vcct_xpl_3d.inp: Three-dimensional model of the SLB specimen using Abaqus/Explicit with VCCT.

References

Mabson, G, “Fracture Interface Elements,” 46th PMC General Session of Mil-17 (Composites Materials Handbook) Organization, Charleston, SC, 2003.

Davidson, B. D., R. Kruger, and M. Konig, “Three-Dimensional Analysis of Center-Delaminated Unidirectional and Multidirectional Single-Leg Bending Specimens,” Composites Science and Technology, vol. 54, pp. 385–394, 1995.

Figures