Thermal-electrical modeling of an automotive fuse

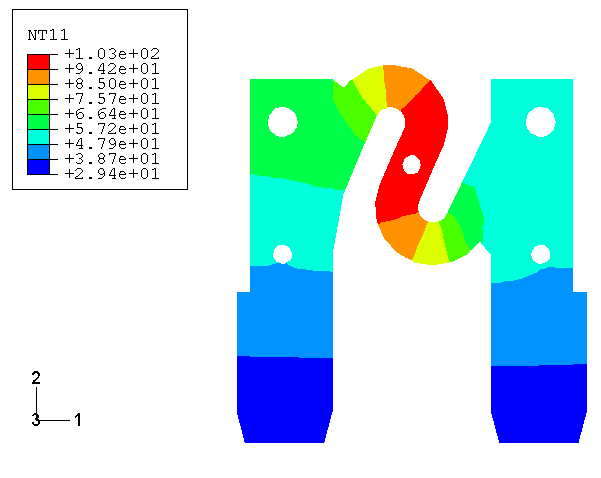
An automotive electrical fuse consists of a metal conductor, such as zinc, embedded within a transparent plastic housing. The plastic housing, which only protects and supports the thin conductor, is not represented in the finite element model. Figure 1 shows front and top sections of the geometry of the conductor. It consists of two 0.76 mm thick blades, with an S-shaped fuse element supported between the blades. The blades fit tightly into standard electrical terminals that are built into the circuit and provide the connection between the electrical circuit and the fuse element. The fuse element is usually much thinner than the fuse blades (in this case 0.28 mm thick) and is designed to melt when the operating current exceeds the design current for a period of time. The fuse blades are 8 mm wide and 30.4 mm long. The fuse element is approximately 3.6 mm wide.

The model is discretized (see Figure 1) with 8-node first-order brick elements (element type DC3D8E), using one element through the thickness. Two 6-node triangular prism elements (element type DC3D6E) are used to fill regions where the geometry precludes the use of brick elements. For comparison refined mesh input files are also included.

The electrical conductivity of zinc varies linearly between 16.75 × 10³ $1/\mathrm{\Omega }$ mm at 20°C and 12.92 × 10³$1/\mathrm{\Omega }$ mm at 100°C. The thermal conductivity varies linearly between 0.1120 W/mm°C at 20°C and 0.1103 W/mm°C at 100°C. The density is 7.14 × 10⁻⁶ kg/mm³, and the specific heat is 388.9 J/kg°C. The fraction of dissipated electrical energy released as heat is specified by the joule heat fraction. We assume that all electrical energy is converted into thermal energy.

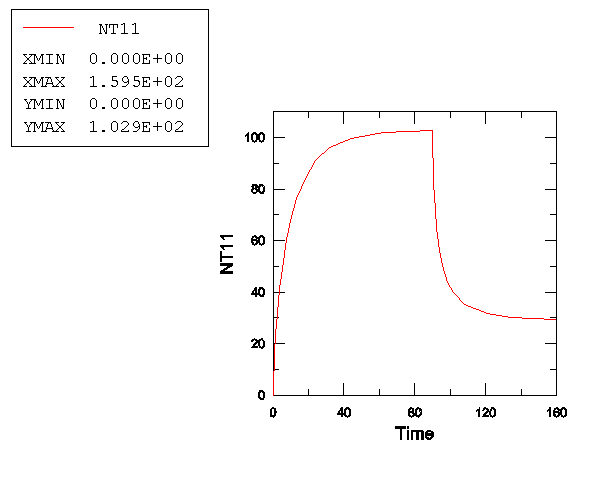
The analysis is done in two steps. In the first step heating of the conductor due to current flow is considered. Once steady-state conditions are reached, the current is switched off and the fuse is allowed to cooldown to the ambient temperature in a second step. During the first part of the analysis, the coupled thermal-electrical equations are solved for both temperature and electrical potential at the nodes using the coupled thermal-electrical procedure. In the subsequent cooldown period, since there is no longer any electric current in the fuse, an uncoupled heat transfer analysis (Uncoupled Heat Transfer Analysis) is performed. The coupled thermal-electrical procedure definition is general enough to request either a steady state or a transient solution; input files illustrating both analysis types are provided. The transient analysis uses an automatic time incrementation scheme that is controlled by specifying the maximum temperature change allowed in an increment to 20°C. The transient analysis is set to terminate when steady-state conditions are reached. Steady state is defined here as the point at which the temperature rate change is less than 0.1°C/s. This condition is defined as part of the definition of the coupled thermal-electrical procedure. We specify a total analysis time of 100 s, with an initial time step size of 0.1 s.

The electrical loading is a steady 30 A current. This is applied as a concentrated current on each of the nodes on the bottom edge of the left-hand-side terminal. The total current and the total heat flux across a section defined through the fuse element are output. The electrical potential (degree of freedom 9) is constrained at the bottom edge of the right-hand-side blade by using a boundary condition (Boundary Conditions). This option is also used to keep the bottom edges of the fuse blades at sink temperatures (degree of freedom 11) of 29.4°C and 30.2°C, respectively.

It is assumed that the exposed metal surfaces lose heat through convection to an ambient temperature of ${\theta }^0=$ 23.3°C. Heat loss from the thin edges is ignored. The film coefficient varies with temperature according to the empirical relation

where $\theta$ is surface temperature (°C); h is the film coefficient (W/mm²°C); and $h^0$ is a constant that depends on the surface geometry—$h^0$ = 4.747 × 10⁻⁶ W/mm² for the blade surfaces, and $h^0$ = 5.756 × 10⁻⁶ W/mm² for the fuse element surfaces. This dependence is entered as a table of film property values in the film coefficient definition (see Thermal Loads).

Mr. Hilali and Dr. Wang of Delphi Packard Electric Systems supplied the geometry of the fuse, the material properties, and the experimental results. Delphi Packard assumes no responsibility for the accuracy of the analysis method or data contained in the analysis.