About Analyzing Variable Dependencies and Equation Incidence

You can work with variable dependencies for normal simulation.

For an example, see Analyzing Variable Dependencies for a Normal Simulation.

You can analyze variable dependencies for a failed initialization of a simulation.

Important: The dependencies for the initialization problem may differ from the dependencies of the simulation problem. To be able to plot variable dependencies after a failed simulation, you must, before the simulation, activate the options: Provide variable dependencies and equation incidence for plotting in the simulation setup, the Debug tab. Store variables after failed initialization in the simulation setup, the Debug tab.

For more information on how to reach these options, see Setting up a Simulation. For more information about the dialog box alternatives, see Simulation Setup Dialog Box.

For an example where the feature of analyzing variable dependencies can be used, see Analyzing Variable Dependencies for a Normal Simulation.

You can work with equation incidence to explore the structure of a translated model. You can also use the equation incidence as a tool for debugging a simulation failure. In this section, you explore the structure of a translated model example using the equation incidence graph.

To display and simulate the model example ControlledTanks1, do the following:

1. Create a function or logical component with a Dymola behavior containing the Dymola model example ControlledTanks1 from the library Modelica_StateGraph2. For more information, see Creating a Function or Logical Component with a Dymola Behavior Containing a Dymola Model Example.
   Note: The full path to the model example is Modelica_StateGraph2.Examples.Applications.ControlledTanks.ControlledTanks1.
2. Display the Simulation Setup dialog box, see Setting up a Simulation. In the Debug tab, activate Provide variable dependencies and equation incidence for plotting.
3. Simulate the model. For more information, see Launching a Virtual Execution.
   Note: The simulation must be finished before analyzing variable dependencies.

The example consists of two tanks, three valves, and a state machine controlling the valves. During simulation, valve1 opens to fill up tank1 with water from the reservoir. When tank1 is full, its content is drained into tank2, making a pause when the former tank is almost empty. Finally, tank2 is emptied and the cycle repeats. To run the example to see how it works, replay the animation. For more information, see Replaying Simulation Results.

To display the equation incidence graph for the model, do the following:

1. Stop the replaying, if you are doing that.
2. From the Signal Monitor, right-click any signal that has dependencies, for example tank1.level, and select Browse Dependencies . The Browse Dependencies dialog box appears.
3. In that dialog box, click Equation incidence. The Equation Incidence window appears, displaying the equation incidence graph for ControlledTanks1.
4. For clarity when explaining, deactivate Rotate the incidence matrix 45°, if activated.

The Equation Incidence window contains three panes. The middle pane displays the dependency graph as a sorted Block Lower Triangular (BLT) form of equation blocks, graphically indicated by nodes. The graph´s diagonal contains either scalars, which are represented as white nodes, or systems of equations, marked by colored nodes. The full color coding of the nodes of the diagonal is:

Table 1.

Color of nodes in the diagonal	Meaning
Green	Linear: Linear systems of equations.
Red	Non-linear: Non-linear system of equations.
Blue	Mixed: Mixed system of equations.
Dark red	Dummy: Dummy derivative system of equations for dynamic state selection.
White	Scalar: Simple scalar equations, including alias equations.

In there are three blue nodes indicating that there are three systems with mixed continuous and discrete equations.

Tip: To display a compact view with condensed trivial systems, activate Compact View. This is a convenient way to see all systems. For the current model the result is:

Now, with none of the above display options activated, click the first blue node, to select the first system, as below:

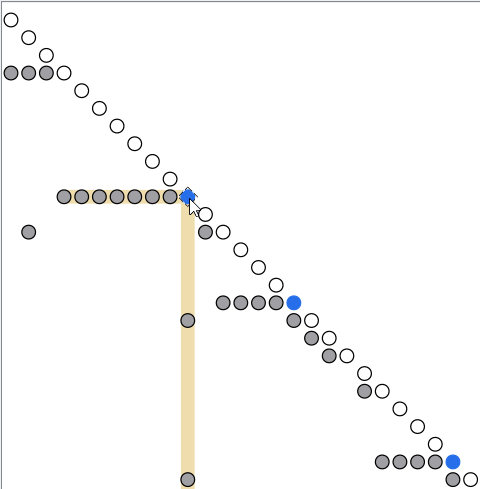In the current model, this example, the upper pane (not displayed in the figure), you get information of what kind of equation block you have selected. In the lower pane (not displayed in the figure below), you get a list of all the variables the equation block solves for. This includes iteration variables, torn variables, as well as discrete variables. For this example, you can see from the list that this system solves for the flow and pressures around valve2, between the two tanks.

The gray off-diagonal nodes represent dependencies. If you click a gray node, you see the corresponding dependency equation in the upper pane.

The gray nodes to the left of the blue node, on the same row, represent variables that need to be computed before the first system can be solved. That is, they represent upstream dependencies for that system. The gray nodes below the blue node, in the same column, show where variables from the first system are used in subsequent computations. That is, they represent downstream dependencies for that system.

An important use of the equation incidence graph is to investigate if the systems are independent of each other. The first system calculated is by definition independent.

To investigate if the second system is independent of the first system, look at the figure above. You can see that the first gray node in the column appears after the line of the second system, meaning that this dependence is not relevant until after the second system has been computed. That is, the second system is independent of the first system.

To investigate if the third system is independent of the second system, select the second system as below:

You can see that the column contains a dependency node just below the system line. To investigate that dependency, select the corresponding node in that row in the diagonal:

You can see that the corresponding column also contains a node directly under the selected node. If you repeat the action by clicking the corresponding node in the diagonal, you still see a node directly under the selected node. But when you repeat the action again, you see the following:

This means that the third system is independent of the second system.

In a similar way, you can prove that the third system is independent of the first system.